Deutsch Algorithm

Implementing 2-qubit Deutsch Algorithm

Initial Problem

Suppose we have a black box that takes in two input bits and produces two output bits. We would like the query the black box as few times as possible to learn what the black box does.

In Deutsch's problem the black box implements one of the following: \[ f_1(x,y) = (x,y)\] \[ f_2(x,y) = (x,\bar{y})\] \[ f_3(x,y) = (x,x \oplus y)\] \[ f_4(x,y) = (x,x \oplus \bar{y})\]

Make it Quantum

We write the four possible functions as unitary matrices operating on the standard computational basis.

\[ U_1 = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \] \[ U_2 = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{bmatrix} \] \[ U_3 = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{bmatrix} \] \[ U_4 = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \] These applied to \( \left|00\right\rangle \), \( \left|01\right\rangle \), \( \left|10\right\rangle \), \( \left|11\right\rangle \) yield the expected result.

Now we can solve this problem in one query if by using a general superposition and manipulation of the two qubits.

Algorithm

We draw the quantum circuit using qasm2circ:

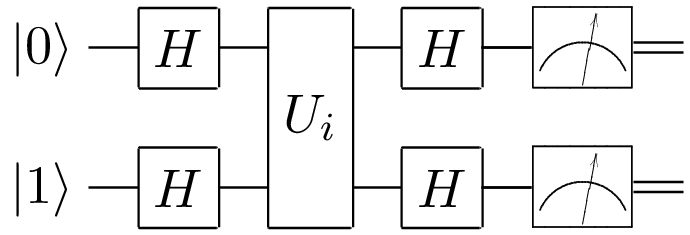
The Hadamard gate is: \[ H = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}\]

When we apply the Hadamard gate: \[ \left|\psi\right\rangle = H\left|0\right\rangle \otimes H \left|1\right\rangle\] \[ = \frac{1}{\sqrt{2}}(\left|0\right\rangle + \left|1\right\rangle) \otimes \frac{1}{\sqrt{2}}(\left|0\right\rangle - \left|1\right\rangle) \] \[ = \frac{1}{2} (\left|00\right\rangle - \left|01\right\rangle + \left|10\right\rangle - \left|11\right\rangle) \]

Now, once we apply \( U_i \) we obtain: \[ \left|\phi_1\right\rangle = U_1 \left|\psi\right\rangle = \frac{1}{2} (\left|00\right\rangle - \left|01\right\rangle + \left|10\right\rangle - \left|11\right\rangle) \] \[ \left|\phi_2\right\rangle = U_2 \left|\psi\right\rangle = \frac{1}{2} (-\left|00\right\rangle + \left|01\right\rangle - \left|10\right\rangle + \left|11\right\rangle) \] \[ \left|\phi_3\right\rangle = U_3 \left|\psi\right\rangle = \frac{1}{2} (\left|00\right\rangle - \left|01\right\rangle - \left|10\right\rangle + \left|11\right\rangle) \] \[ \left|\phi_4\right\rangle = U_4 \left|\psi\right\rangle = \frac{1}{2} (-\left|00\right\rangle + \left|01\right\rangle + \left|10\right\rangle - \left|11\right\rangle) \]

We finish off with the final Hadamard Gates: \[ H \otimes H = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & -1 & 1 & -1 \\ 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 \end{bmatrix} \]

Thus, finally: \[ \left|o_1\right\rangle = (H\otimes H)U_1\left|\psi\right\rangle = \left|01\right\rangle\] \[ \left|o_2\right\rangle = (H\otimes H)U_2\left|\psi\right\rangle = -\left|01\right\rangle\] \[ \left|o_3\right\rangle = (H\otimes H)U_3\left|\psi\right\rangle = \left|11\right\rangle\] \[ \left|o_4\right\rangle = (H\otimes H)U_4\left|\psi\right\rangle = -\left|11\right\rangle\]

This is great, we can figure out the black box by observing the first bit.

Visualization

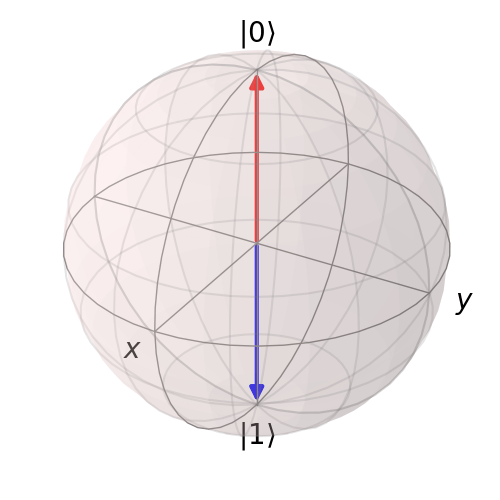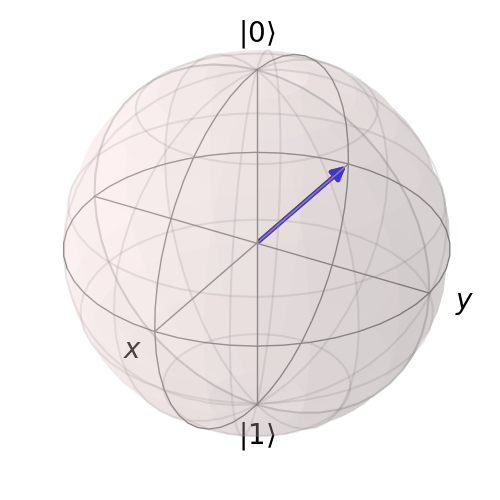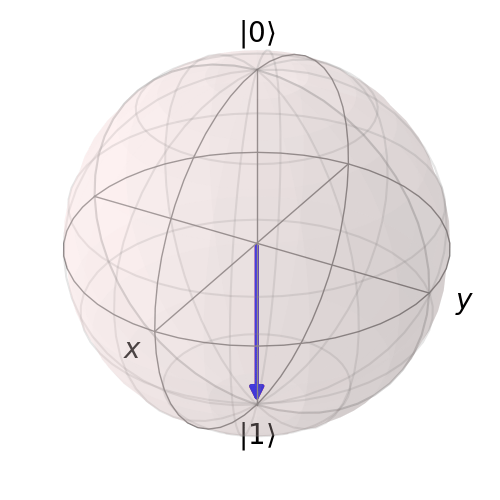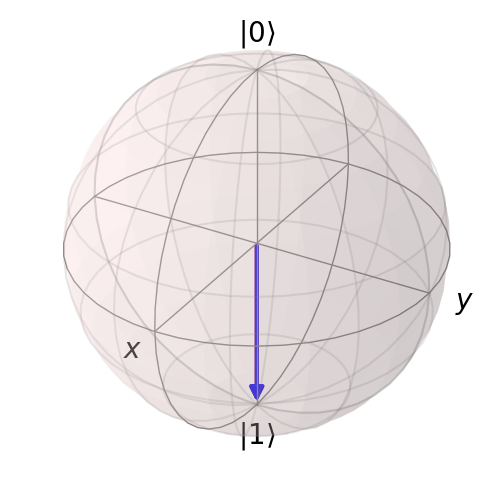
Let's draw the states as we evolve in time with the circuit. As an example, lets use \( U_2\).

We start with \[ \left|\psi\right\rangle = (H \otimes H) (\left|0\right\rangle \otimes \left|1\right\rangle) \] \[ = (H \otimes H) \begin{pmatrix} 1 \\ 0 \end{pmatrix} \otimes \begin{pmatrix} 0 \\ 1 \end{pmatrix} \] \[ = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & -1 & 1 & -1 \\ 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 \end{bmatrix} \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} \] \[= \frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ -1 \\ 1 \\ -1 \end{pmatrix}\]

The density matrix is \[ \left|\psi \right\rangle \left\langle\psi\right| = \frac{1}{4}\begin{bmatrix} 1 & -1 & 1 & -1 \\ -1 & 1 & -1 & 1 \\ 1 & -1 & 1 & -1 \\ -1 & 1 & -1 & 1 \end{bmatrix} \]

For practice we take the partial trace and draw the mapped density matrix to the Bloch sphere. We then apply \( U_2\) to \( \left|\psi \right\rangle\). And once again draw to the Bloch Sphere.

Finally, we apply \( H \otimes H\) and draw to the Bloch Sphere.

For \(U_2\) we obtain the following animation:

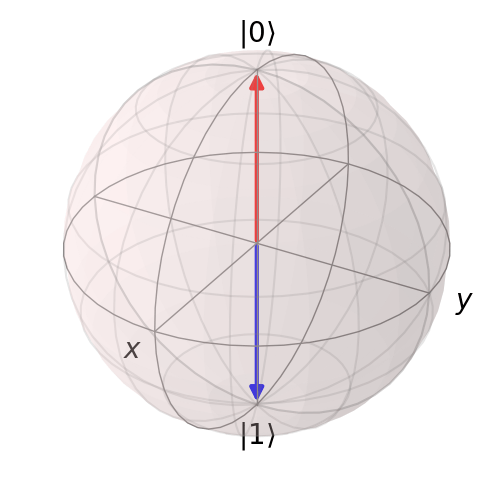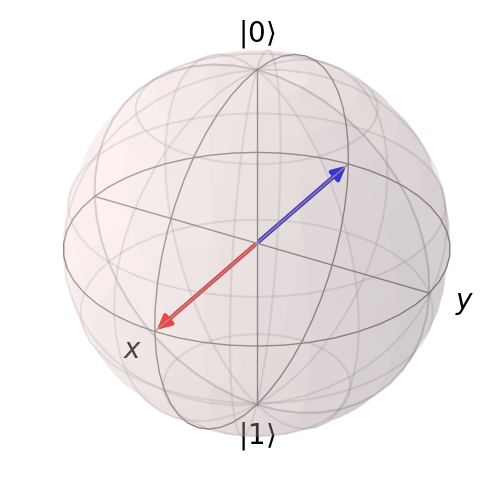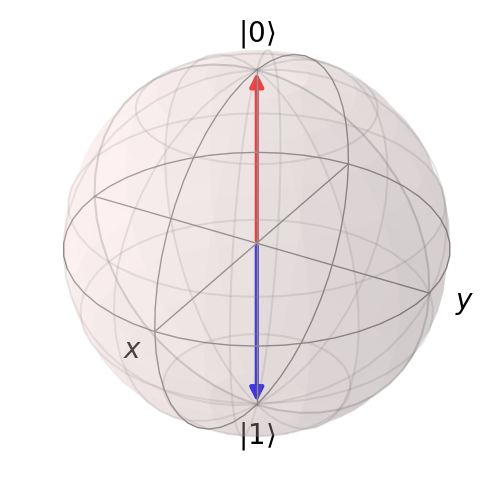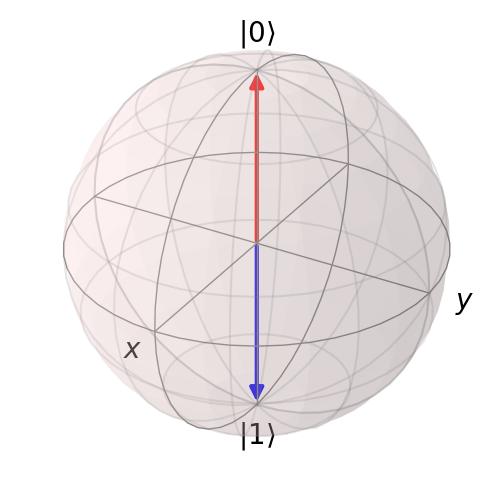
Following similar procedure for \(U_4\) we obtain the following animation: