Exploiting quantum entanglement

TL;DR: Quantum entanglement an interesting concept in physics, and gives rise to a counterintuitive nature of our universe: nonlocal realism. I show a way to make use of entanglement to prepare arbitrary quantum states on today's contemporary quantum computers.

Quantum entanglement is one of the most fascinating and counterintuitive concepts in modern physics. It is a phenomenon that occurs when two or more particles become correlated in such a way that their properties are dependent on each other, even when separated by large distances. This means that measuring one particle can instantly affect the state of the other, regardless of the distance between them. The intention of this blog post is to first talk about how entanglement changes our understanding of the universe (local realism), then I describe a peculiar implication of utilizing entanglement for the task of state preparation for quantum computers (my latest research.)

'Quantum entanglement' generated by Stable diffusion model

1. A note on the nature of our universe

While the idea of entanglement might seem like something out of science fiction, it has been experimentally confirmed and is now a key concept in quantum mechanics. However, it raises some profound and intriguing questions about the nature of reality itself.

One of the most interesting questions that entanglement raises is the idea of local realism. Local realism is the idea that the properties of particles exist independently of any measurement or observation, and that they have definite values even when not being measured. This concept is in contrast to the view of quantum mechanics, which suggests that the properties of particles do not have definite values until they are measured, and that the act of measurement itself affects the properties of the particles!

As we observe our daily lives, we make some assumptions about reality: (1) a thing is changed only when it is touched, and (2) things are real and exist in the universe independent of our minds. This assumption is termed "local realism" and is broken thanks to quantum entanglement.

Addressing this dilemma of local vs nonlocal realism seems philosophical, but it also has real implications. Can we develop some experiment that will objectively prove whether our universe is locally real? In 2022, the Nobel Prize in Physics was equally split to John Clauser, Alain Aspect and Anton Zeilinger who developed experiments that prove our universe is not locally real. This gives us understanding of entanglement and makes fields such as quantum computing and quantum information science possible.

2. State preparation of quantum computers

Let me begin by quoting Schrödinger with remarks to the EPR Paradox:

It is rather discomforting that the theory should allow a system to be steered or piloted into one or the other type of state at the experimenter’s mercy in spite of his having no access to it. -- E. Schrödinger, 1935.

First, he essentially notes the intriguing "nonlocal realism" property that is brought by quantum entanglement. But secondly, he coined this term of "quantum steering" whereby, in a sense, we can control one particle by measuring a different, yet entangled, particle. I will show later how we can make use of quantum steering to do useful tasks!

Criteria for quantum computers

Quantum computers operate on qubits and can be in a superposition of states. Quantum gates act on the qubits to change the state. Experimentally, DiVincenzo's criteria provide the conditions necessary for realizing quantum computation:

1. A scalable physical system with well-characterized qubit
2. The ability to initialize the state of the qubits to a simple fiducial state
3. Long relevant decoherence times
4. A "universal" set of quantum gates
5. A qubit-specific measurement capability

Let's zoom into condition 2: how do we prepare qubits to be in a simple state -- i.e., a "state reset"? Well, today's quantum computers implement one of two methods:

Passive Reset: were we let our system of qubits equilibrate (thermalize) with the environment. This poses some issues when condition 3 requires long qubit lifetimes, as our qubits will interact with the environment and decay before we can get any work done! Or in other words, as our technologies improve it may take longer to wait for qubits to equilibrate with the environment than compared to the actual quantum computation!

Analogy: During a cold day, the temperature of a house get colder and colder until it is the same temperature as the outdoors.

Active Reset: we measure the qubits and correct the result of a quantum flip gate depending on the readout. We need a classical computer to process the readout and check if we should apply the flip gate. However, now we are introducing a bit of latency with the classical computer in the loop (think of having to do this with thousands of qubits!). Measurement itself can be error-prone which may give incorrect readouts.

Analogy: We add an air conditioner to the house, with a thermometer, that will cool the house.

Another dilemma is that both active reset and passive reset only initialize one particular state: $\ket{0}$. What if we wanted an arbitrary state, $\ket{\psi}$? Well, traditionally, this is where we apply quantum gates to transform our $\ket{0}$ state to an arbitrary $\ket{\psi}$ state: $\ket{\psi} = U \ket{0}$. But with thousands of qubits, and a complex quantum system, a universal gateset would require intense calibration.

State preparation on quantum computers via quantum steering

Now let me describe a method demonstrated in my recent paper where we exploit quantum entanglement to prepare arbitrary quantum states. The key idea is to entangle two particles: one which we call an "ancilla" and one our "system." We entangle them in a specific way, dependent on what state we wish to prepare our system. Then we measure the ancilla, and due to the particles being entangled, this will cause our system particle to be "kicked" into a particular intermediate state. The ancilla is then reset to a simple state. We repeat this process of entangling the two particles and measuring. This whole process can be summarized pictorially where $U$ is the operation that entangles the ancilla and system particles:

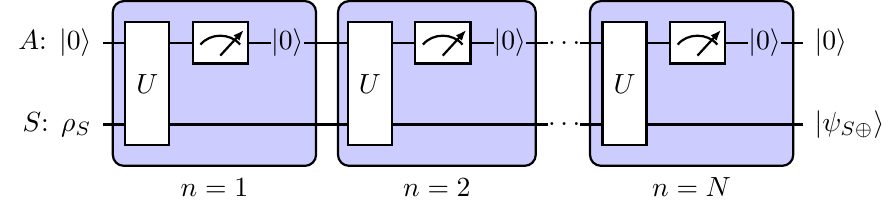
Now, we let the quantum computer implement the specific entangling operation $U$ where the qubits act as particles. We use IBM Quantum computers and show how the intermediate state of our system state changes over time. Here's a visualization on the Bloch sphere:

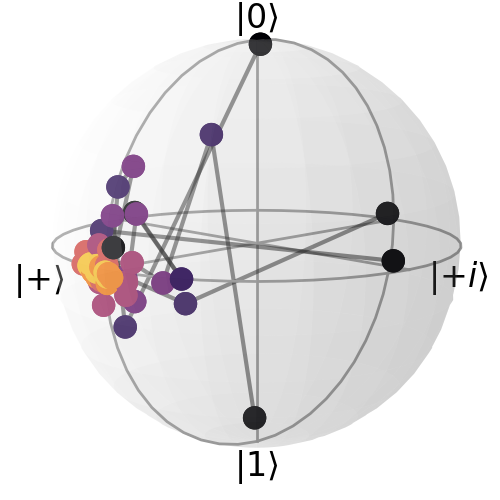
The black dots show the initial states, while the yellow dots are the final states. We see that the state of our qubit converges to a single point on the Bloch sphere -- our desired state $\ket{+}$ (I've chosen $\ket{+}$ as a demonstration, but any desired target state would reveal the same result.) And this convergence does not depend on the initial state!

Something I haven't discussed is what kind of entanglement operations ($U$) you would need to implement this protocol. It turns out, we can describe the "non-local" entangling parts of a two-qubit operation inside a Weyl Chamber tetrahedron:

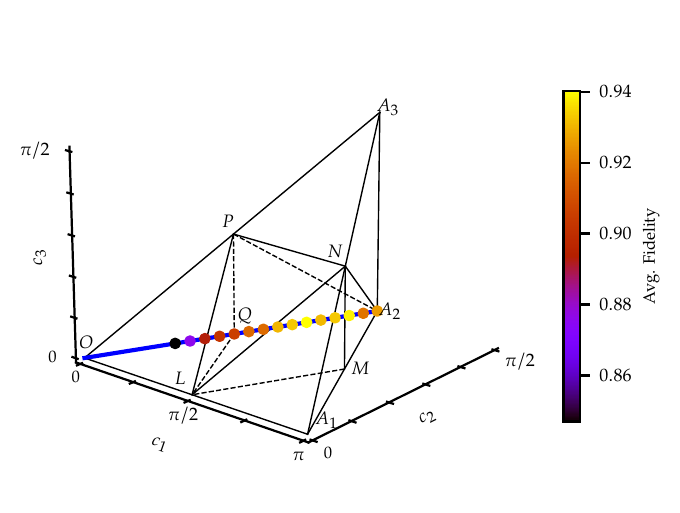
The blue line represents all possible entangling operations that will satisfy the task of state preparation (any arbitrary state!). The dots show how well that specific usage of an entangling operation was able to prepare a final arbitrary state on a specific IBM Quantum computer.

Conclusion

State preparation of a quantum computer is difficult task as it conflicts with the goal of having long-lived and stable qubits. But by utilizing the properties of entanglement, we can prepare a system qubit that can be protected while we conduct measurements on an ancilla qubit that is exposed to an environment. Perhaps future quantum technologies can be designed in this way!