Having some fun with Julia and simulating a Wave packet in 2D.

Main Idea

We will evolve the wavepacket in 2D by taking the tensor products between two 1D (x,y) spaces.

Wavepacket

The wavepacket is expressed as a Gaussian:

\[\Psi(x) = \frac{\sqrt{\Delta x}}{\pi^{1/4}\sqrt{\sigma}} e^{i p_0 (x-\frac{x_0}{2}) - \frac{(x-x_0)^2}{2 \sigma^2}}\]

With the basis spanning the 1D space. And total state is represented by \(\Psi = \Psi_x \otimes \Psi_y\)

Hamiltonian

The kinetic energy term is p_x^2/2 and p_y^2/2. The two-dimensional potential is a boundary with two slits.

function potential(x,y)
        if x > 20 && x < 25 && abs(y) > 1 && abs(y) < 5
                return 0
        elseif x > 20 && x < 25
                return 150
        elseif x > 48
                return 150
        else
                return 0
        end
end

I also use a gaussian potential:

potential(x,y) = exp(-(x^2 + y^2)/15.0)

Time Evolution

At first, I had some trouble with installing DifferntialEquations.jl due to compilation errors for Arpack.jl. So I decided to just solve it manually by separating the real and imaginary components for the state, and then preforming the Discrete Laplace Operator for finite differences. Followed by adding the potential part. This is what I got:

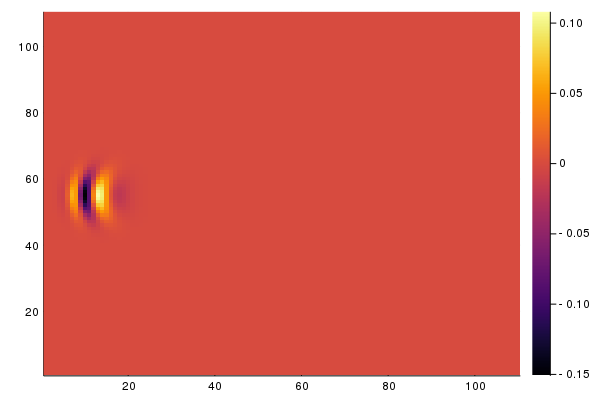
However, before I began working on visualization, Arpack.jl mysteriously compiled (probably because I switched to the official binary of Julia, rather than compiling my own). So I started exploring DifferntialEquations.jl. I then discovered QuantumOptics.jl which makes it pretty easy to simulate various quantum systems, so decided I should use it. It comes with a nice timeevolution.schroedinger which will evolve (integrate) the system.

Double Split starts with:

x0 = -5
y0 = 0
p0_x = 3.0
p0_y = 0.0
σ = 2.0

Guassian starts with:

x0 = -5
y0 = 0
p0_x = 1.5
p0_y = -.5
σ = 2.0

Results

Julia has very nice support for plotting and animations. I abuse this here. Moreover, due to the Julia pre-compilation step, as long as you do not abuse the global space too much, the processing is rather quick.

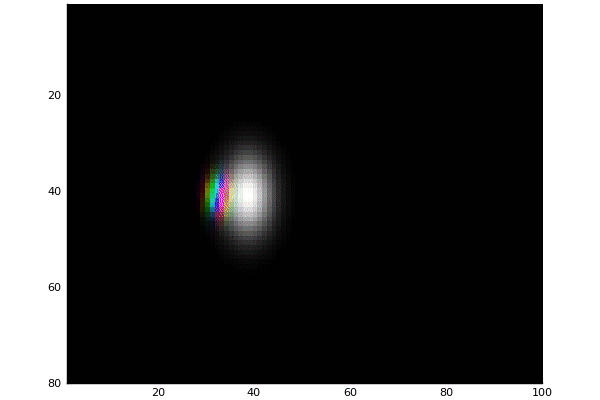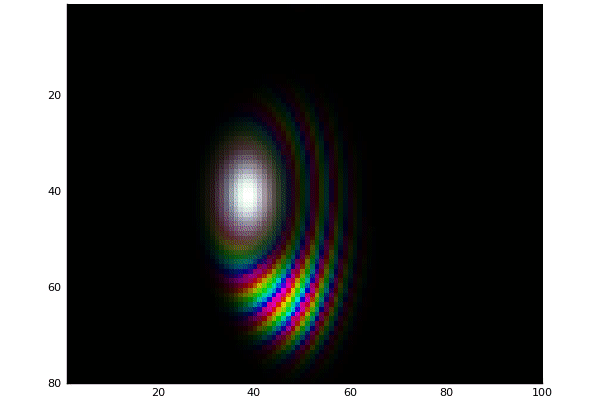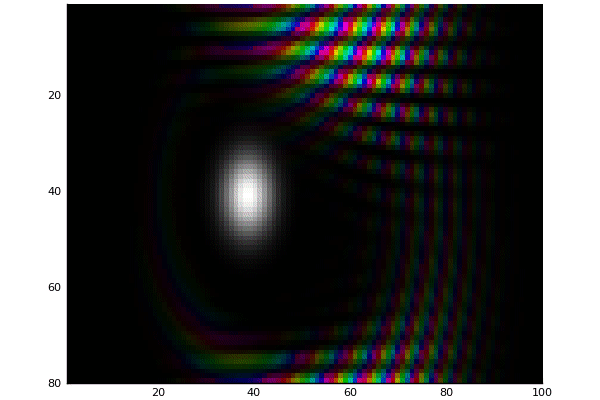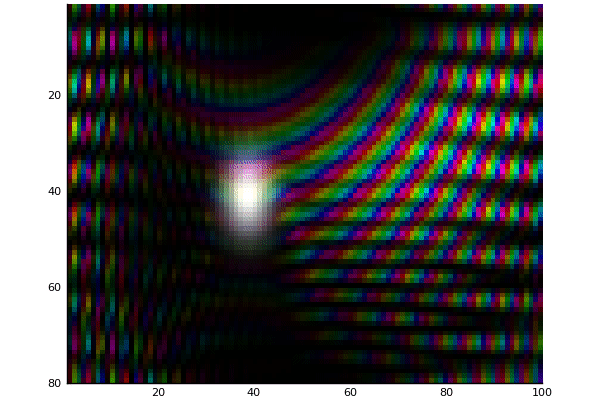
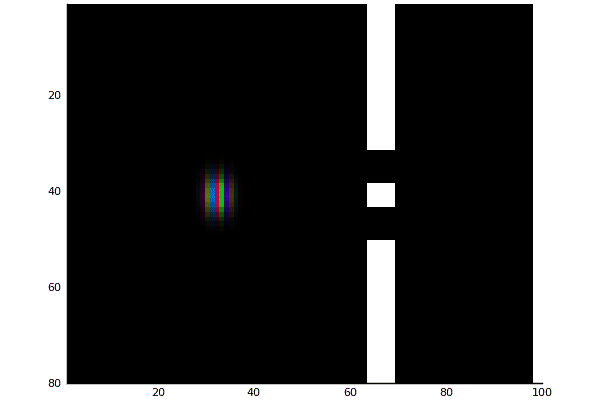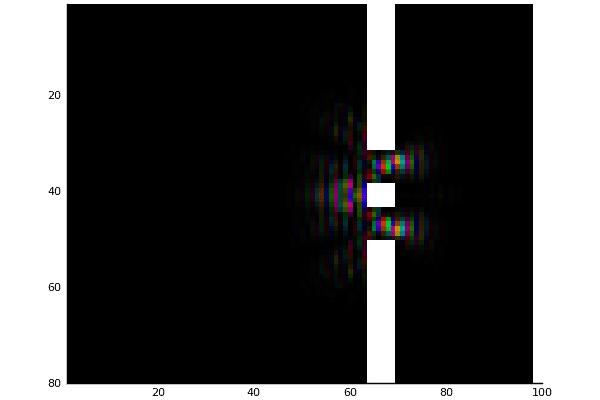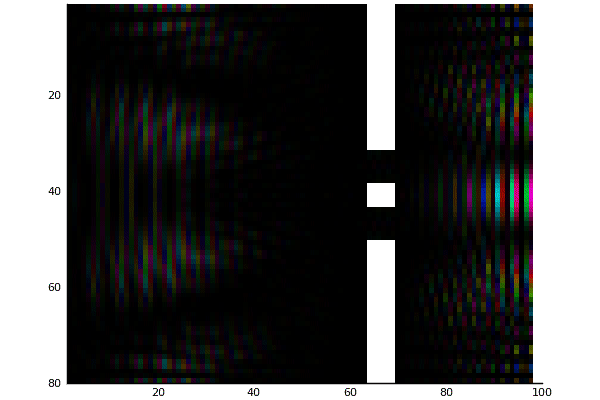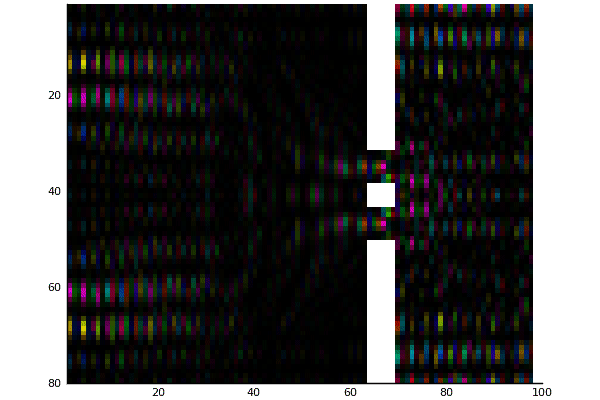
Double Slit potential with magnitude mapped to color

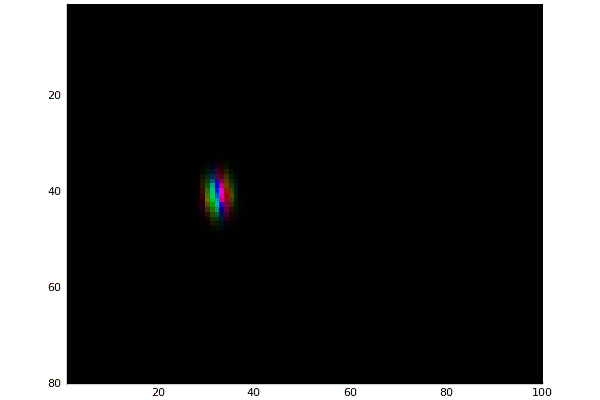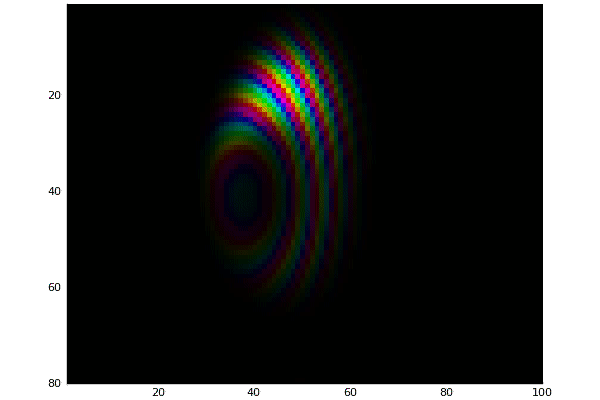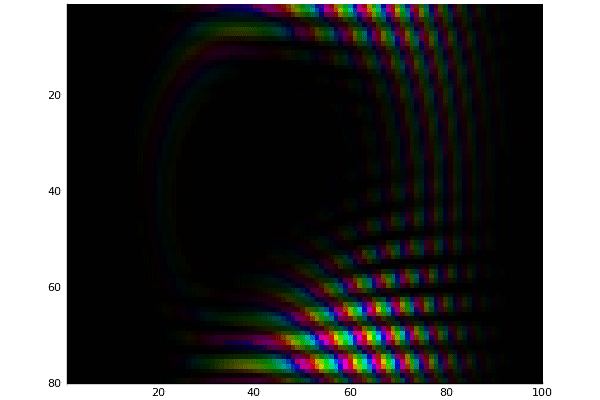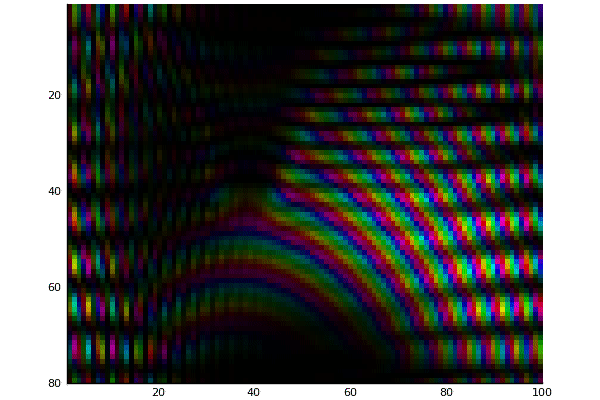
Gaussian Potential

Represent phase as hue and magnitude as value (HSV)

Decided this is not enough to show the true "wave" nature as the visualization neglects the actual phase component... So time for more color!

Double Slit potential

Gaussian Potential

HSV and Showing Potential

Guess this would be a good time to actually visualize the of potential, and get our final nice visualization

Double Slit potential

Gaussian potential